Για να κατανοήσουμε την τριγωνομετρία, τα μαθηματικά πρέπει να προσεγγιστούν με νέες προοπτικές. Ο προσδιορισμός αυτής της προοπτικής μπορεί να είναι οδυνηρός, αλλά ευχάριστος. Εάν βλέπετε τα μαθηματικά με τρόμο και ανασφάλεια, αυτό το άρθρο θα βοηθήσει ελπίζουμε να γίνετε πιο αισιόδοξοι για την έναρξη μιας τάξης τριγωνομετρίας.
Παρουσιάζεται περίπλοκη λογική
Όταν μπήκα στο κολέγιο, δεν πήρα μαθηματικά. Παρόλο που οι επιστήμες με ενδιέφεραν, έτρεξα από αυτούς και στα χέρια της λογοτεχνίας και της φιλοσοφίας, οπότε δεν θα έπρεπε να αντιμετωπίσω τέσσερα εξάμηνα του λογισμού. Όμως, στο τελευταίο εξάμηνο της προπτυχιακής μου εργασίας, εγώ εγγραφή σε μια μαθηματική τάξη φιλοσοφίας. Έμεινα έκπληκτος από την περίπλοκη λογική που παρουσιάστηκε. Προσπάθησα για έναν τρόπο να χωρίσω κάθε πρόβλημα στα πιο στοιχειώδη μέρη και στη συνέχεια τα συγκέντρωσα για να δημιουργήσω μια λύση.
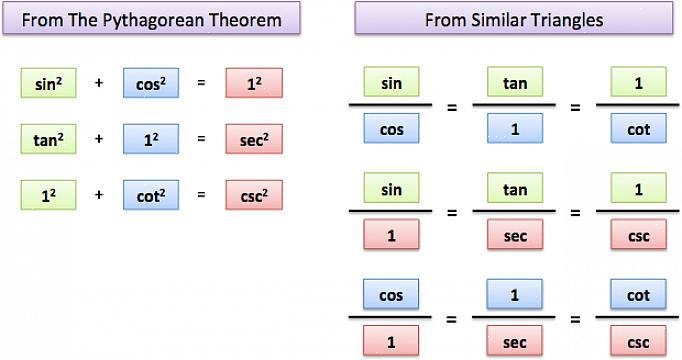
Το κλειδί για την κατανόηση της τριγωνομετρίας, είναι να θυμόμαστε ότι τα μαθηματικά ακολουθούν ένα απλό σύνολο κανόνων. Οι αρχές της τριγωνομετρίας βασίζονται στον προσδιορισμό της σχέσης των σημείων σε έναν κύκλο. Για να αποκτήσετε τον άξονα-x του κύκλου, χρησιμοποιείτε το ημιτονοειδές και χρησιμοποιείτε τη συνάρτηση sine = το μήκος του άξονα γ / την υποτείνουσα. Cosine = ο άξονας x / η υπόταση, και η εφαπτομένη υπολογίζεται χρησιμοποιώντας το Πυθαγόρειο Θεώρημα. Μόλις κατανοηθούν αυτοί οι κανόνες, τότε γίνεται μια απλή κατασκευή βασισμένη στους κανόνες της λογικής. Εδώ θέτει τη δημιουργικότητα που ενσωματώνεται στα μαθηματικά.
Λύνω προβλήματα
Διασπώντας το ημιτονοειδές, το συνημίτονο, και εφαπτόμαστε σε μια πιο απλοϊκή γλώσσα και μαθαίνοντας πώς μπορούμε να εφαρμόσουμε αυτούς τους τύπους ρεαλιστικά, αντί να τις θεωρούμε ως έννοιες με τις οποίες έχουμε κολλήσει στην τάξη, μπορούμε να αρχίσουμε να αντιλαμβανόμαστε τη λειτουργία τους και να αρχίσουμε να κατανοούμε πώς να χρησιμοποιήσετε την τριγωνομετρία για την επίλυση προβλημάτων.
Αν δίδαξα κλάσματα σε παιδιά, θα τους δείξω μια πίτσα κομμένη σε 8 φέτες. Στη συνέχεια, θα αφαιρούσα τμήματα της πίτσας και θα ρωτούσα τον μαθητή πόσα είχαμε απομείνει από ολόκληρη την πίτσα. Αμετάβλητα, τα παιδιά θα μπορούσαν να κατανοήσουν αυτήν την ιδέα πιο γρήγορα από ό, τι αν απλά περιέγραφα τα κλάσματα χωρίς σημείο αναφοράς. Ομοίως, πρέπει να απεικονίσουμε τη χρησιμότητα των τριγωνομετρικών συστημάτων για να τα καταλάβουμε πραγματικά. Απομνημονεύστε τους έξι βασικούς τύπους λαμβάνοντας υπόψη αυτό το τρίγωνο. Αυτά είναι τα στοιχεία της τριγωνομετρίας.
Θα δυσκολευτείτε να κατανοήσετε την τριγωνομετρία. Συνεργαστείτε με τους δασκάλους και τους δασκάλους σας για να ανακαλύψετε πώς να εφαρμόσετε τις βασικές αρχές της τριγωνομετρίας στη δική σας ζωή. Όταν η τριγωνομετρία μπορεί να εφαρμοστεί σε πτυχές της καθημερινής σας ζωής, η μάθηση γίνεται ευκολότερη. Τα μαθηματικά μπορούν να είναι διασκεδαστικά αν καταλάβετε τη δημιουργική του πτυχή. Δουλέψτε σκληρά για να καταλάβετε την τριγωνομετρία και θα αποκτήσετε μια εικόνα για έναν εντελώς διαφορετικό κόσμο σκέψης.