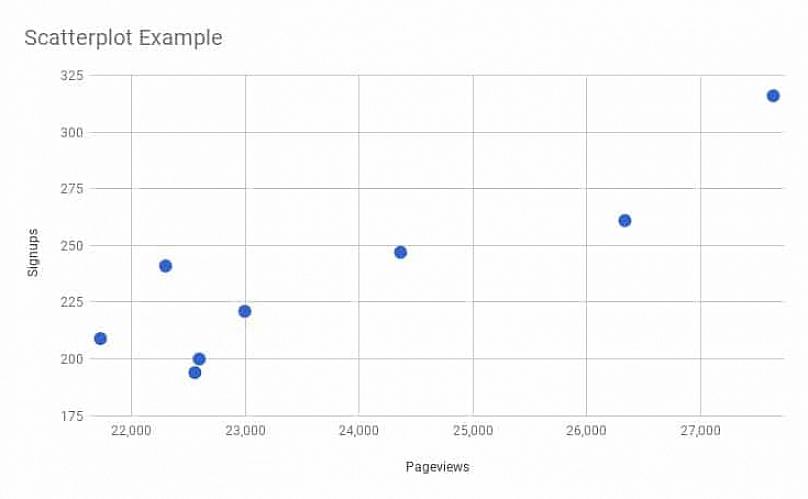
Ένα διάγραμμα διασποράς είναι ένας τύπος γραφήματος που σχετίζεται με δύο ζευγάρια συνόλων δεδομένων. Είναι χρήσιμο για την προσπάθεια εύρεσης της συσχέτισης μεταξύ των δύο συνόλων δεδομένων. Δείτε πώς μπορείτε να δημιουργήσετε ένα διάγραμμα διασποράς:
- Σχεδιάστε ένα πλέγμα. Πρώτα, σχεδιάστε μια οριζόντια γραμμή (X Άξονας). Στη συνέχεια, σχεδιάστε μια κάθετη γραμμή (Υ άξονας) που τέμνει το κέντρο της οριζόντιας γραμμής. Αυτό γίνεται καλύτερα σε χαρτί γραφήματος, επειδή θα μπορείτε να σχεδιάσετε με ακρίβεια κάθε σημείο δεδομένων αντί να μαντέψετε την κατά προσέγγιση θέση του. Εάν όλα τα σημεία δεδομένων σας είναι θετικοί αριθμοί και όχι αρνητικοί, δεν χρειάζεστε ολόκληρο το πλέγμα. Αντ 'αυτού, σχεδιάστε ένα σχήμα L στραμμένο προς τα δεξιά. Το κάτω άκρο του L είναι ο άξονας X και το κατακόρυφο άκρο είναι ο άξονας Υ.
- Επισημάνετε κάθε άξονα. Η κλίμακα που χρησιμοποιείτε εξαρτάται από τα δεδομένα που πρέπει να σχεδιάσετε. Για παράδειγμα, η κλίμακα σας μπορεί να κυμαίνεται από 1 έως 10, με ετικέτες σε κάθε ακέραιο αριθμό. Μπορεί να κυμαίνεται από 1 έως 100, με ετικέτες σε κάθε 10 αριθμούς. Μπορεί να κυμαίνεται από 0 έως 1, με ετικέτες κάθε 0,1.
- Σχεδιάστε τα σημεία δεδομένων. Η πρώτη στήλη δεδομένων σχετίζεται με τον προσανατολισμό του σημείου δεδομένων κατά μήκος του άξονα Χ. Η δεύτερη στήλη αναφέρεται στον προσανατολισμό της κατά μήκος του άξονα Υ. Για παράδειγμα, εάν το σημείο δεδομένων είναι (35), θα πρέπει να γραφεί 3 μονάδες στα δεξιά του σημείου όπου ο άξονας Χ και Υ διασχίζουν και πέντε μονάδες προς τα πάνω. Κάθε σημείο πρέπει να αντιπροσωπεύεται από μια μικρή κουκκίδα ή ένα σύμβολο Χ. Εάν έχετε δύο σύνολα δεδομένων που δεν είναι ήδη γραμμένα με τη μορφή (35), ο οριζόντιος άξονας πρέπει να είναι η ανεξάρτητη μεταβλητή ή αυτή που πιστεύετε ότι προκάλεσε την άλλη. Ο κάθετος άξονας είναι η εξαρτώμενη μεταβλητή ή αυτή που πιστεύετε ότι προκλήθηκε από το άλλο σύνολο δεδομένων.
- Δείτε τα αποτελέσματα. Εάν τα αποτελέσματα φαίνονται ομαδοποιημένα κατά μήκος μιας γραμμής ή παραβολής (σχήμα U ή V), υπάρχει ισχυρή συσχέτιση μεταξύ των δύο συνόλων δεδομένων. Εάν δεν φαίνεται να σχετίζονται, η συσχέτιση μεταξύ των δύο συνόλων δεδομένων είναι αδύναμη ή μπορεί να μην υπάρχει καμία συσχέτιση. Εάν συσχετίζονται έντονα και σχηματίζουν μια απότομη κλίση, τότε μια αλλαγή στην πρώτη μεταβλητή επηρεάζει σημαντικά τη δεύτερη μεταβλητή. Εάν η κλίση είναι σχεδόν επίπεδη (οριζόντια), μια μεγάλη αλλαγή στην πρώτη μεταβλητή θα επηρεάσει λίγο τη δεύτερη μεταβλητή.
Το διάγραμμα διασποράς ή το διάγραμμα διασποράς χρησιμοποιείται συχνά σε τάξεις άλγεβρας, αλλά υπάρχουν πολλές εφαρμογές πραγματικού κόσμου. Για παράδειγμα, κάποιος μπορεί να σχεδιάσει τις ώρες ύπνου που λαμβάνουν οι μαθητές το βράδυ πριν από την εξέταση με τη βαθμολογία τους στην εξέταση για να δούμε αν η ποσότητα του ύπνου φαίνεται να προκαλεί αλλαγή στη βαθμολογία των εξετάσεων.