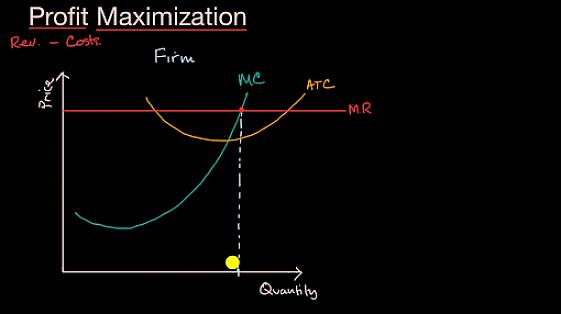
Ένα από τα πρώτα πράγματα που προκύπτει σε μια κατηγορία Οικονομικής Διοίκησης είναι η απόφαση για το πώς να μεγιστοποιήσετε τα κέρδη και να δημιουργήσετε ένα μοντέλο μεγιστοποίησης κέρδους. Αυτό είναι ένα διαφορετικό ζήτημα από τη μεγιστοποίηση των εσόδων, καθώς είναι τα κέρδη που συνήθως προσπαθούμε να μεγιστοποιήσουμε.
Το καλό σημείο στη μεγιστοποίηση των κερδών είναι να βρείτε το σημείο όπου τα οριακά σας έσοδα ισούνται με το οριακό κόστος σας. Το οριακό κόστος σας είναι το κόστος δημιουργίας ενός επιπλέον αντικειμένου. γενικά, αυτό θα είναι επίσης το μεταβλητό κόστος κατασκευής ενός αντικειμένου. Για παράδειγμα, αν σας κοστίζει 0,40€ σε προμήθειες και εργασία για να φτιάξετε ένα χάμπουργκερ, το οριακό κόστος ενός χάμπουργκερ είναι 0,40€
Οριακά έσοδα
Τα οριακά σας έσοδα είναι ένα πιο δύσκολο θηρίο. Εάν βρίσκεστε σε μια πολύ ανταγωνιστική βιομηχανία και το προϊόν είναι κοινόχρηστο ή "fungible" στο econ-speak, συχνά θα πρέπει να λάβετε ό, τι ισχύει για το προϊόν σας. Σε αυτήν την περίπτωση, η τρέχουσα τιμή είναι τα οριακά σας έσοδα.
Εάν πουλάτε κάτι που δεν είναι γενικό, ώστε οι πελάτες να έχουν ζήτηση για το προϊόν σας συγκεκριμένα, θα έχετε μια συνάρτηση ζήτησης (ή καμπύλη ζήτησης) για το προϊόν σας, όπου μετράμε τη ζήτηση ενός προϊόντος ως συνάρτηση της τιμής. Εάν έχουμε P ως τιμή και Q ως ποσότητα, θα έχουμε συνάρτηση ζήτησης P = a-bQ. καθώς η ποσότητα αυξάνεται, η τιμή μειώνεται, καθώς θα πάρει μια χαμηλότερη τιμή για να ωθήσει τους ανθρώπους να αγοράσουν περισσότερο από ένα προϊόν.
Τα έσοδά σας είναι η τιμή επί της ποσότητας ή P * Q. Δεδομένου ότι τώρα P, μπορούμε να δηλώσουμε τα έσοδα ως aQ-bQ ^ 2 (χρησιμοποιώντας ^ ως τον εκθετικό όρο όπως στο Excel). Τα οριακά έσοδα, χρησιμοποιώντας βασικά παράγωγα λογισμού, είναι a-2bQ. Η λειτουργία οριακών εσόδων σας θα έχει πάντα το διπλάσιο της καμπύλης της ζήτησης.
Συνάρτηση οριακών εσόδων
Ας πούμε ότι έχουμε μια συνάρτηση ζήτησης για burgers P = 4-0,1Q. Η συνάρτηση οριακών εσόδων θα είναι 4-0,2Q, δίνοντας τα πράγματα διπλάσια από την κλίση της συνάρτησης ζήτησης.
Στη συνέχεια, δημιουργήσαμε ένα κατάστημα όπου τα οριακά έσοδα ισούνται με το οριακό κόστος. Εάν έχουμε οριακό κόστος 0,5, τότε 4-0,2Q = 0,5, 0,2Q = 3,5 ή Q = 17,5. Στη συνέχεια, πυροβολήσαμε για να πουλήσουμε 17,5 μπιφτέκια ανά περίοδο και στη συνέχεια να συνδέσουμε 17,5 στη λειτουργία ζήτησης, θα έχουμε μια στοχευμένη τιμή 4-0,1 * 17,5 ή 1,70€ ένα μπιφτέκι.
Το σημείο όπου τα οριακά έσοδα ισούται με το οριακό κόστος μας δίνει το σημείο όπου το οριακό κέρδος είναι ίσο με μηδέν και το οριακό κέρδος σας είναι μηδέν όπου μεγιστοποιείτε τα κέρδη σας. Η εύρεση αυτού του σημείου είναι πώς μπορείτε να μεγιστοποιήσετε τα κέρδη.